机器学习的三要素
机器学习方法通常由模型、策略和算法三部分组成:模型+策略+算法
模型
定义:输入空间到输出空间的映射关系。学习过程即为从假设空间中搜索出适合当前数据的假设。
策略
定义:从假设空间众多的假设中选择到最优的模型的学习标准或规则。
要从假设空间中选择到最优的模型,需要解决以下问题:
1.评估某个模型对单个训练样本的效果
2.评估某个模型对训练集的整体效果
3.评估某个模型对包括训练集、预测集在内的所有数据的整体效果
衡量效果的指标
损失函数(Loss Function)
定义:用来衡量预测结果与真实结果之间的差距,值越小,代表预测结果与真实结果越一致。通常是一个非负实值函数,记作L(Y,f(x))。通过各种方式缩小损失函数的过程被称为优化。
损失函数曲线图:
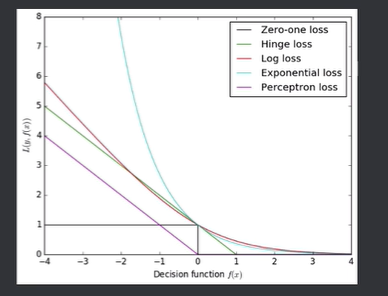
0-1损失函数(0-1 LF)
定义:预测值和实际值精确相等则 “没有损失” 为 0,否则意味着 “完全损失”(如函数1)。为 1预测值和实际值精确相等有些过于严格,可以采用两者的差小于某个阈值的方式(如函数2)。
适用场景:理想状况模型
函数1:L(Y,f(X)) = \begin{cases} 1, & Y \neq f(X) \\ 0, & Y = f(X) \end{cases} 函数2:L(Y,f(X)) = \begin{cases} 1, & |Y - f(X)| \geq T \\ 0, & |Y - f(X)| < T \end{cases}
示例:
Y:真实结果
f(x):预测结果
L:完全损失的0-1损失函数(函数1)
L' :以T作为阈值的损失函数(函数2)
L相当于L' 的一种特殊情况,即T=0时,两者等价
绝对损失函数(Absolute LF)
定义:预测结果与真实结果差的绝对值
函数:L(Y,f(X)) = |Y - f(X)|
平方损失函数(Quadratic LF)
定义:预测结果与真实结果差的平方。
函数:L(Y,f(X)) = (Y - f(X))^{2}
适用场景:线性回归
优点:
每个样本的误差都是正的,累加不会抵消
平方对于大误差的惩罚大于小误差
数学计算简单友好,倒数为一次函数
对数损失函数(Logarithmic LF)
定义:也称对数似然损失函数 (log-likehood loss function),定义为L(Y,P(Y|X)) = -\log P(Y|X),其中P是条件概率。对数函数具有单调性,在求最优化问题时,结果与原始目标一致。可将乘法转化为加法,简化计算。
函数:L(Y,P(Y|X)) = -\log P(Y|X)
适用场景:逻辑回归、交叉熵
对于二分类问题,设样本真实标签 y∈{0,1},模型预测样本属于正类的概率为 p=P(y=1∣x),那么单个样本的对数损失函数为:
对于多分类问题,假设类别数为 K,样本真实标签 y 是一个 K 维的 one - hot 向量,模型预测样本属于第 i 类的概率为 pi=P(yi=1∣x),i=1,2,⋯,K ,则单个样本的对数损失函数为:
指数损失函数(Exponential LF)
定义:定义为L(Y,f(x)) = e^{-Y*f(x)},其中 Y 是样本的真实标签 ,通常取值为+1或−1(在二分类问题中常见),f(X)是模型对于样本X的预测值。。具有单调性、非负性的优良性质,使得越接近正确结果误差越小。
函数:L(Y,f(x)) = e^{-Y*f(x)}
适用场景:AdaBostting
折页损失函数(Hinge LF)
定义:也称铰链损失,对于判定边界附近的点的惩罚力度较高,常见于 SVM。
函数:L(f(x)) = \max(0,1 - f(x))
适用场景:SVM、softmargin
风险函数
定义:
经验风险(Empirical Risk)
定义:损失函数度量了单个样本的预测结果,要想衡量整个训练集的预测值与真实值的差异,将整个训练集所有记录均进行一次预测,求取损失函数,将所有值累加,即为经验风险。经验风险越小说明模型 f(x)对训练集的拟合程度越好。
函数:R_{emp}(f) =\frac{1}{N}\sum_{i = 1}^{N}L(Y,f(x))
期望风险(Risk Function)
定义:所有数据集(包括训练集和预测集,遵循联合分布 P (X,Y))的损失函数的期望值。
公式:R_{exp}(f) =\iint L(Y,f(x))P(x,y)dxdy
经验风险和期望风险的对比:
经验风险存在的问题:在样本过小时,仅关注经验风险,很容易导致过拟合。
已知7个点坐标数据作为训练集(x=1~7),分别对这些数据进行回归,得到几个模型如下图
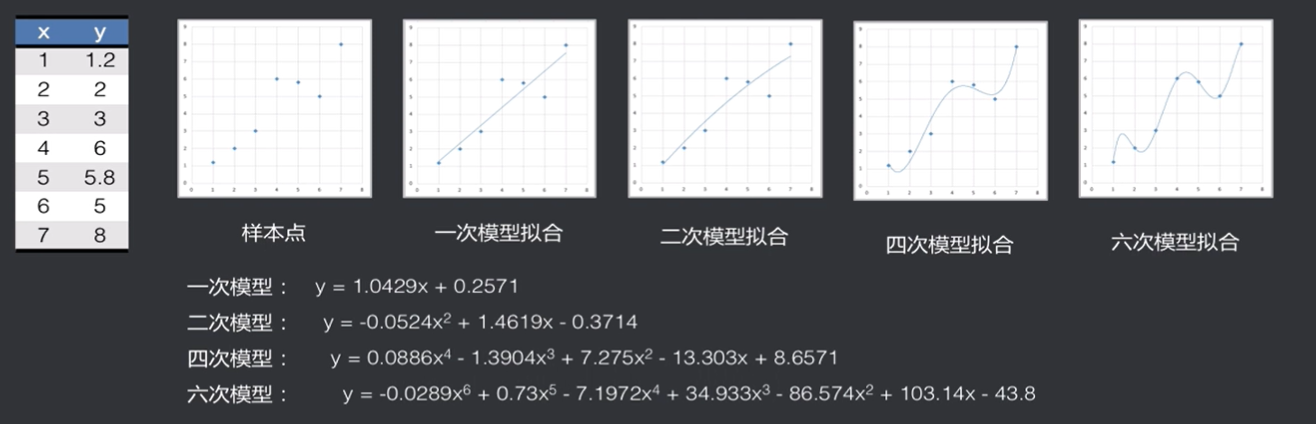 增加三个点作为预测集(x=8~9),对训练集和全局(训练集+预测集)进行预测,通过损失函数(绝对值损失函数)累加求平均得到各个经验风险(标黄处)和期望风险(标红处)如下图
增加三个点作为预测集(x=8~9),对训练集和全局(训练集+预测集)进行预测,通过损失函数(绝对值损失函数)累加求平均得到各个经验风险(标黄处)和期望风险(标红处)如下图
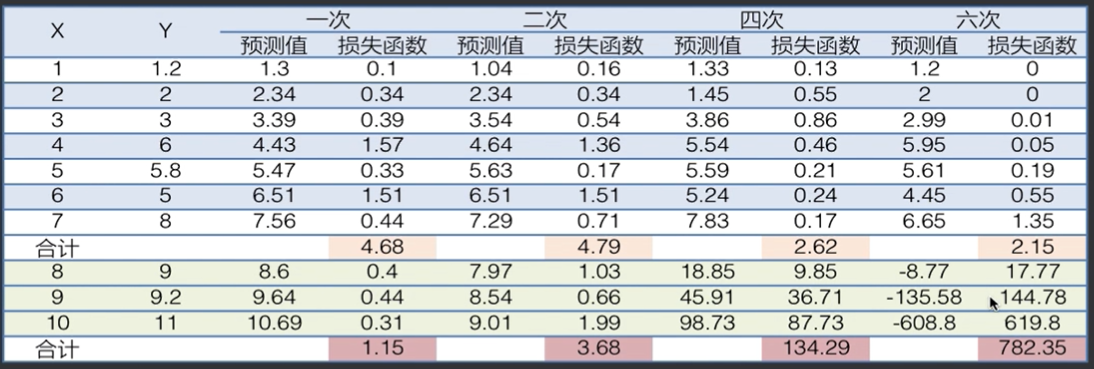 可以发现,六次模型虽然经验风险最低,但其期望风险确实最高,这个时候六次模型就是过拟合模型。由于期望风险是通过全局进行计算的,全局中的预测集无法拿到(只有在作出预测的时候此时预测的数据才是预测集),所以就需要引入下面的结构风险。
可以发现,六次模型虽然经验风险最低,但其期望风险确实最高,这个时候六次模型就是过拟合模型。由于期望风险是通过全局进行计算的,全局中的预测集无法拿到(只有在作出预测的时候此时预测的数据才是预测集),所以就需要引入下面的结构风险。
结构风险(Structural Risk)
定义:在经验风险的基础上,增加一个正则化项(Regularizer)或者叫做惩罚项(Penalty Term),公式为:(R_{srm}(f)=\frac{1}{N}\sum_{i = 1}^{N}L(Y,f(x))+\lambda J(f)) ,其中 λ 为一个大于 0 的系数,J (f) 表示模型 f (x) 的复杂度。也就是说结构风险 = 经验风险 + 复杂度。
函数:(R_{srm}(f)=\frac{1}{N}\sum_{i = 1}^{N}L(Y,f(x))+\lambda J(f))
正则化项:即惩罚函数,该项对模型向量进行惩罚,从而避免过拟合问题。正则化方法会自动削弱不重要的特征变量,自动从许多的特征变量中 “提取” 重要的特征变量,减小特征变量的数量级。简单来说正则化项 = 复杂度 = 惩罚函数 = \lambda J(f)=\lambda\sum_{i = 1}^{n}|\theta_{i}|,其中\theta_{i}为模型函数的参数
以下图训练集为例,X为自变量,Y为因变量(真实值),使用一次模型和六次模型通过绝对值损失函数计算它们的经验风险R_{emp}(f)。
| X | Y | 一次 | 六次 | ||
|---|---|---|---|---|---|
| 预测值 | 损失函数 | 预测值 | 损失函数 | ||
| 1 | 1.2 | 1.3 | 0.1 | 1.2 | 0 |
| 2 | 2 | 2.34 | 0.34 | 2 | 0 |
| 3 | 3 | 3.39 | 0.39 | 2.99 | 0.01 |
| 4 | 6 | 4.43 | 1.57 | 5.95 | 0.05 |
| 5 | 5.8 | 5.47 | 0.33 | 5.61 | 0.19 |
| 6 | 5 | 6.51 | 1.51 | 4.45 | 0.55 |
| 7 | 8 | 7.56 | 0.44 | 6.65 | 1.35 |
| 合计 | 4.68 | 2.15 | |||
然后通过函数 \lambda J(f)=\lambda\sum_{i = 1}^{n}|\theta_{i}|计算模型的复杂度(\lambda取值为1,\theta_{i}为模型函数的参数)
可以得出(R_{srm}(f_{一次模型})=\frac{1}{N}\sum_{i = 1}^{N}L(Y,f(x))+\lambda J(f)) =\frac{1}{7} \times 4.68 + 1\times1.0429\approx1.7114
(R_{srm}(f_{六次模型})=\frac{1}{N}\sum_{i = 1}^{N}L(Y,f(x))+\lambda J(f)) =\frac{1}{7} \times 2.15 + 1\times(|-0.0289| + |0.732|+|-7.1972|+|34.933|+|- 86.574|+|103.14|)\approx232.91 得出结论:虽然六次模型的经验风险小于六次模型,但是六次模型因为多了很多参数导致结构化风险特别大,遇到新数据的时候风险也会很大,出现了过拟合的现象,所以在选择模型的时候此时优先选择一次模型。
经验风险和结构风险的关系:
1.经验风险越小,模型决策函数越复杂(J (f) 越大),其包含的参数越多
2.当经验风险函数小到一定程度就出现了过拟合现象
3.防止过拟合现象的方式,就要降低决策函数的复杂度(J (f) ),让惩罚项 J (f) 最小化,需要同时保证经验风险函数和模型决策函数的复杂度都达到最小化,把两个式子融合成一个式子得到结构风险函数然后对这个结构风险函数进行最小化
范数:TODO
基本策略
经验风险最小(EMR : Empirical Risk Minimization)
结构风险最小(SRM : Structural Risk Minimization)
算法
模型的选择与评估
模型的选择原则
模型选择(Model Selection):针对某个具体的任务,通常会有多种模型可供选择,对同一个模型也会有多组参数,可以通过分析、评估模型的泛化误差,选择泛化误差最小的模型。
图中蓝色虚线为训练误差,绿色实现为泛化误差,选择泛化误差最小的位置(红色竖线处)即为模型选择的基本原则。其中红色竖线左边是欠拟合,右边是过拟合,随着拟合程度的增加,训练误差一直降低直至趋近于0,泛化误差先降低后增加,红色竖线处即为泛化误差最低点。
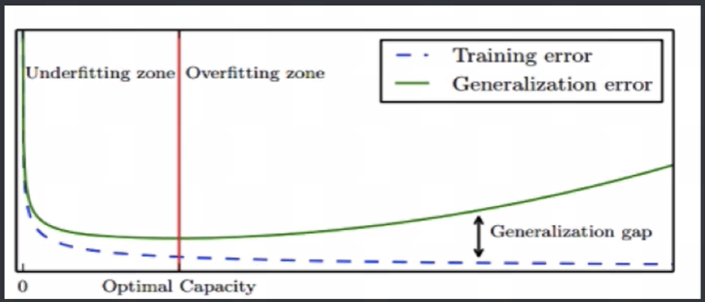
误差(Error):是模型的预测输出值与其真实值之间的差异。
训练(Training):通过已知的样本数据进行学习,从而得到模型的过程。
训练误差(Training Error):模型作用于训练集时的误差。
泛化(Generalize):由具体的、个别的扩大为一般的,即从特殊到一般,称为泛化。对机
器学习的模型来讲,泛化是指模型作用于新的样本数据(非训练集)。
泛化误差(Generalization Error):模型作用于新的样本数据时的误差。

模型容量(Model Capacity):是指其拟合各种模型的能力。
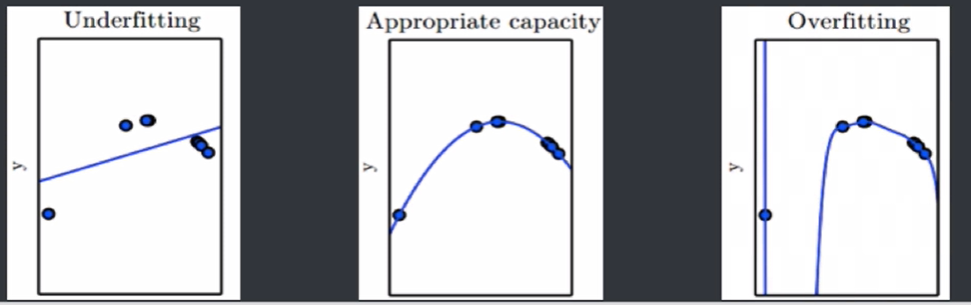
过拟合(Overfitting):是某个模型在训练集上表现很好,但是在新样本上表现差。模型将训练集的特征学习的太好,导致一些非普遍规律被模型接纳和体现,从而在训练集上表现好,但是对于新样本表现差。反之则称为欠拟合(Underfitting),即模型对训练集的一般性质学习较差,模型作用于训练集时表现不好。
 模型的评估方法
模型的评估方法
评估思路
通过实验测试,对模型的泛化误差进行评估,选出泛化误差最小的模型。待测数据集全集未知(因为全集=训练集+预测集,预测集多数情况下是未知),将已知数据集划分为训练集和测试集,使用测试集进行泛化测试,测试误差(Testing Error)即为泛化误差的近似。
 需要注意的点:
需要注意的点:
1.测试集与训练集尽可能互斥(无交集)
2.测试集与训练集独立(没有依赖关系)同分布(数据分布一致)
评估方法
留出法(Hold-out )
定义:将已知数据集分成两个互斥的部分,其中一部分用来训练模型,另一部分用来测试模型,评估其误差,作为泛化误差的估计。
需要注意的点:
1.两个数据集的划分要尽可能保持数据分布一致性,避免因数据划分过程引入为的偏差。保持样本的类别(比如男女、老幼、身高段)比例相似,即采用分层采样(Stratified Sampling)。

2.数据分割存在多种形式会导致不同的训练集、测试集划分,单次留出法结果往往存在偶然性,其稳定性较差,通常会进行若干次随机划分、重复实验评估取平均值作为评估结果。
3.数据集拆分成两部分,每部分的规模设置会影响评估结果,测试、训练的比例通常为 7:3、8:2 等
优点:
实现简单、方便,在一定程度上能评估泛化误差
测试集和训练集分开,缓解了过拟合
缺点:
一次划分,评估结果偶然性大
数据被拆分后,用于训练、测试的数据更少了
适用场景:已知数据集数量充足
交叉验证法(Cross Validation):
定义:将数据集划分 k 个大小相似的互斥的数据子集,子集数据尽可能保证数据分布的一致性(分层采样),每次从中选取一个数据集作为测试集,其余用作训练集,可以进行 k 次训练和测试,得到评估均值。该验证方法也称作 k 折交叉验证(k-fold Cross Validation)。使用不同的划分,重复 p 次,称为 p 次 k 折交叉验证。

优点:
k 可以根据实际情况设置,充分利用了所有样本
多次划分,评估结果相对稳定
缺点:
计算比较繁琐,需要进行 k 次训练和评估
适用场景:已知数据集数量充足
留一法(Leave-One-Out, LOO)
定义:是 k 折交叉验证的特殊形式,将数据集分成两个,其中一个数据集记录条数为 1,作为测试集使用,其余记录作为训练集训练模型。
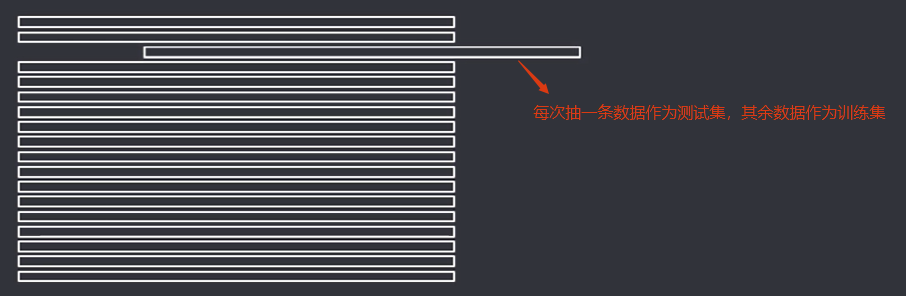
特点:留一法是特殊的交叉验证法。不同的是交叉验证法是把数据集分为k份,每份有一条或多条数据;而留一法是把数据集分为两份,一份只有一条数据,另一份是其他数据。
优点:训练出的模型和使用全部数据集训练得到的模型接近,其评估结果比较准确
缺点:当数据集较大时,训练次数和计算规模较大
适用场景:已知数据集较小且可以有效划分训练集 / 测试集
自助法(Bootstrapping)
定义:是一种产生样本的抽样方法,其实质是有放回的随机抽样。从已知数据集中随机抽取一条记录,然后将该记录放入测试集同时放回原数据集,继续下一次抽样,直到测试集中的数据条数满足要求。
假设已知数据集 D 含有 n 条,采用自助法得到一个记录条数为 n 的测试集 T。D 中的一些数据会在 T 中出 现多次,还有一些数据不会出现。
估算一下经过 n 次有放回采样后,大概多少记录未被选中:
某一次具体的采样,一条数据被选中的概率为 1/n,未被选中的概率为:1 - 1/n
连续 n 次采样均未被选中的概率为:(1 - 1/n)ⁿ,取极限:\lim_{n \to \infty}(1 - \frac{1}{n})^n = \frac{1}{e} \approx 0.368
通过有放回的抽样获得的训练集(未被选中过的数据,总量的2/3)去训练模型,不在训练集中的数据(选中过的数据,总量的 1/3 )去用于测试,这样的测试结果被称作包外估计(Out-of-Bag Estimate,OOB)
优点:
样本量较小时可以通过自助法产生多个自助样本集,且有约 36.8% 的测试样本
对于总体的理论分布没有要求
缺点:
无放回抽样引入了额外的偏差
适用场景:已知数据集较小且难以有效划分训练集 / 测试集
模型的性能度量
定义:评价模型泛化能力的标准。对于不同的模型,有不同的评价标准,不同的评价标准将导致不同的评价结果。模型的好坏是相对的,取决于对于当前任务需求的完成情况。
回归算法常用的性能度量
回归算法的性能度量通常选用均方误差(Mean Squared Error)。
给定样例集 D = (\{(x_1,y_1), (x_2,y_2),\cdots, (x_m,y_m)\}),模型为f,其性能度量均方误差为E(f;D)=\frac{1}{m}\sum_{i = 1}^{m}(f(x_i)-y_i)^2
具体的样例集假定为:
| x | y |
|---|---|
| 58 | 116 |
| 59 | 118 |
| 60 | 120 |
| 63 | 132 |
根据样例集设计了两个模型分别为:
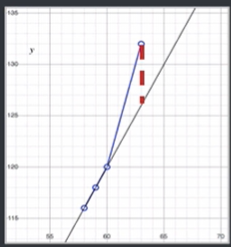
f_1=2x
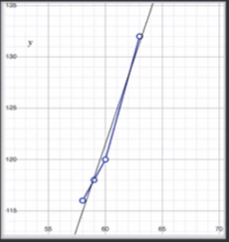
f_2=3.286x-75.643
使用均方误差作为性能度量:
E(f_1;D)=\frac{1}{m}\sum_{i = 1}^{m}(f_1(x_i)-y_i)^2=\frac{1}{4}[(2∗58−116)^2 +(2∗59−118)^2+(2∗60−120)^2
+(2∗63−132)^2
]=\frac{1}{4}(0+0+0+36)=9
E(f_1;D)=\frac{1}{m}\sum_{i = 1}^{m}(f_1(x_i)-y_i)^2=\frac{1}{4}*\{[(3.286*58 -75.643) -116]^2 +[(3.286*59 -75.643) -118]^2 +[(3.286*60 -75.643) -120]^2 +[(3.286*63 -75.643) -132]^2 \}=\frac{1}{4}*3.8583=0.964575
比较两个模型的均方误差E(f_1;D)和E(f_2;D),显然是E(f_2;D)更小,也就是说两个模型在整个样例集中的表现是第二个模型好于第一个模型
分类算法常用的性能度量:
错误率:分类错误的样本占总样本数的比例,其公式为 :E(f;D)=\frac{1}{m}\sum_{i = 1}^{m}I(f(x_i)\neq y_i)
精度:分类正确的样本占总样本数的比例,其公式为 :acc(f;D)=\frac{1}{m}\sum_{i = 1}^{m}I(f(x_i)= y_i)=1 - E(f;D)
查准率:预测结果为正的样本中实际值也为正的比例
查全率:实际值为正的样本中被预测为正的样本的比例
P-R 曲线:查准率 - 查询率曲线
混淆矩阵:将预测分类结果和实际分类结果做成矩阵的形式显示
F_{\beta}-score:\beta值的不同体现了对查全率和查准率的不同倾向,其公式为 :F_{\beta}=\frac{(1 + \beta^2)*P*R}{\beta^2*P + R}
受试者特征曲线(ROC)和曲线下面积(AUC):TPR-FPR 曲线(真正例率 - 假正例率曲线 )
代价曲线:不同类型的预测错误对结果影响不同而增加代价(cost),绘制P(+)cost - cost_{norm}曲线
......
聚类算法常用的性能度量
外部指标(External Index):将聚类结果同某个参考模型进行比较
Jaccard 系数(Jaccard Coefficient,JC):JC = \frac{a}{a + b + c}
FM 指数(Fowlkes and Mallows Index,FMI):FMI = \sqrt{\frac{a}{a + b} * \frac{a}{a + c}}
Rand 指数(Rand Index,RI):RI = \frac{2(a + d)}{m(m - 1)}
内部指标(Internal Index):不使用参考模型直接考察聚类结果
DB 指数(Davise - Bouldin Index,DBI):DBI = \frac{1}{k}\sum_{i = 1}^{k}\max_{j \neq i}(\frac{avg(C_i)+avg(C_j)}{d_{cen}(\mu_i,\mu_j)})
Dunn 指数(Dunn Index,DI):DI = \min\limits_{1 \leq i \leq k}\left\{\min\limits_{j \neq i}\left(\frac{d_{min}(C_i,C_j)}{\max\limits_{1 \leq l \leq k}diam(c_l)}\right)\right\}
模型的比较检验
选择合适的评估方法和相应的性能度量,计算出性能度量后直接比较。
存在以下问题:
1.模型评估得到的是测试集上的性能,并非严格意义上的泛化性能,两者并不完全相同
2.测试集上的性能与样本选取关系很大,不同的划分,测试结果会不同,比较缺乏稳定性
3.很多模型本身有随机性,即使参数和数据集相同,其运行结果也存在差异
把上述问题按照统计学的知识描述一下: 已知两个模型f_1和f_2,两者的泛化性能在测试集上的表现不同,f_1好于f_2,请检验在统计意义上f_1是否好于f_2?这个把握有多大?
关于以上问题可以在小故事(《女士品茶》掷硬币故事的统计学分析)中寻求答案。
统计假设检验(Hypothesis Test):
定义:事先对总体的参数或者分布做一个假设,然后基于已有的样本数据去判断这个假设是否合理。即样本和总体假设之间的不同是纯属机会变异(因为随机性误差导致的不同),还是两者确实不同。常用的假设检验方法有t-检验法、χ2检验法(卡方检验)、F-检验法等。
基本思想:
- 从样本推断整体
- 通过反正法推断假设是否成立
- 小概率事件(一般取0.05)在一次试验中基本不会发生
- 不轻易拒绝原假设
- 通过显著性水平定义小概率事件不可能发生的概率
- 全称命题只能被否定而不能被证明(只能证伪不能证明)
假设检验步骤:
1.建立假设:
根据具体的问题,建立假设:
原假设(Null Hypothesis):搜集证据希望推翻的假设,记作 H₀
备择假设(Alternative Hypothesis):搜集证据予以支持的假设,记作 H₁
假设的形式:
- 双尾检验:H₀ : μ = μ₀,H₁ : μ ≠ μ₀ 不等于、有差异
- 左侧单尾检验:H₀ : μ ≥ μ₀,H₁ : μ < μ₀ 降低、减少
- 右侧单尾检验:H₀ : μ ≤ μ₀,H₁ : μ > μ₀ 提高,增加
只有小概率事件发生了,才拒绝原假设,检验过程保护原假设
2.确定检验水准:
检验水准(Size of a Test):又称显著性水平(Significance Level),记作 α,是指原假设正确,但是最终被拒绝的概率。
在做检验的过程中,会犯两种错误:
原假设为真,被拒绝,称作第一类错误,其概率记作 α,即为显著性水平,取值通常为 0.05、0.025,0.01 等
原假设为假,被接受,称作第二类错误,其概率记作 β,即为检验功效(power of a test)
显著水平 α=0.05 的意思是:在原假设正确的情况下进行 100 次抽样,有 5 次错误的拒绝了原假设。
3.构造统计量:
根据资料类型、研究设计方案和统计推断的目的,选用适当检验方法和计算相应的统计量。
常见检验方法:
- t检验:小样本(<30),总体标准差σ未知的正态分布
- F检验:即方差分析,检验两个正态随机变量的总体方差是否相等的一种假设检验方法
- Z检验:大样本(>=30)平均值差异性检测,又称u检验
- χ2检验:即卡方检验,用于非参数检验,主要是比较两个及两个以上样本率以及两个分类变量的关联性分析



评论区